物質の状態と力学的性質
気体を除く物質の状態には、液体と固体、さらに、これらの中間的な性質を示すゲルやゾルがあります。
これらの状態はすべて、液体の性質の粘性と固体の性質の弾性を併せ持ち、その状態や力学的性質は、粘性と弾性の大きさとバランスで決まります。

固 体

ゲ ル

ゾ ル

液 体
力学特性の評価
材料の力学特性は、加えた変形に対する応力、あるいは、加えた荷重に対する変形量から算出します。
代表的な力学パラメータとして、固体の性質である弾性と、液体の性質である粘性があります。
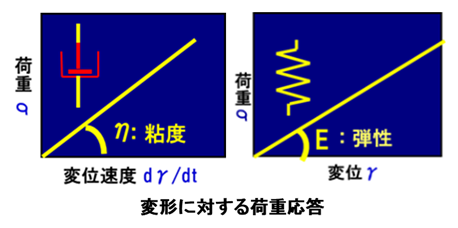
粘性: σ=η・dγ/dt ニュートンの法則・・・粘度測定
弾性: σ=E・γ フックの法則 ・・・弾性測定
変形を与えた時の変形速度及び変形量に対する荷重応答曲線
の傾きから、それぞれの粘性η 及び弾性E を取得できます。
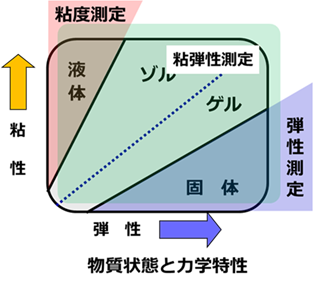
物質の固液状態は、粘性と弾性物質ンスによって決まるため、粘性・弾性の両方を持つ物質の評価には粘弾性測定が最適
動的粘弾性測定
固体に対する力学特性評価では、サンプルに定速変形を加えたときの応力(又は、定荷重を加えたときの変形)より、弾性パラメータを求め、液体の場合、定速変形を加えたときの応力から粘性パラメータを求めます。このように定速変形を加えて調べる測定は静的粘弾性測定と呼ばれます。これらの測定では、サンプルを理想弾性体やニュートン流体と見なし、力学パラメータを算出します。
動的粘弾性測定では、正弦波形の連続変形を加えたときの応力波形を測定し、弾性率と粘性率を同時に取得する測定技術です。
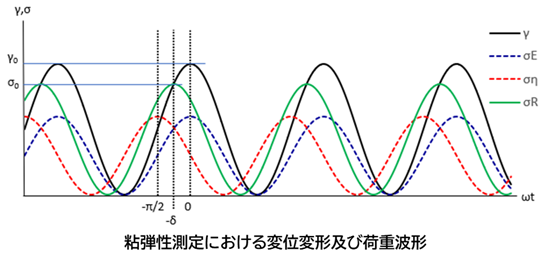
σ= m・E’・γ0・sin ωt + m・E”・γ0・cos ωt = m・σ0・sin (ωt+δ) ・・・ m:形状係数
動的粘弾性測定の理論
粘弾性体に正弦波形の変形を加えた場合、弾性応答σEは同位相、粘性応答σηはπ/2進んで発現し(時間軸では戻る)、これらの合成波が荷重応答波形として観測されている。
荷重応答波形と検出位相差δから、弾性応答分と粘性応答分に分離して粘弾性パラメータ の貯蔵弾性率 E’(G’)、損失弾性率 E”(G”)、損失弾性率 tanδ(=E”/E’、G”/G’)を求める。
E:体積変化を伴う変形(圧縮、引張、曲げ)におけるパラメータ
G:剪断変形におけるパラメータ
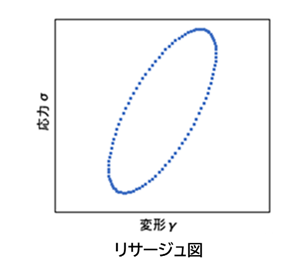
リサージュ図
動的粘弾性測定は変形時に構造変化のない線形領域内で行う必要があり、応力σ/変形γの関係図が、円(液体)、楕円(粘弾性体)、直線(固体)のいずれかであることを確認する。